
Introduction . Cryptology , i.e., the science of ciphers, has applied since the very beginning some mathematical methods, mainly the elements of probability theory an statistics. Mechanical and electromechanical ciphering devices, introduced to practice in the twenties of our century, broadened considerably the field of applications of mathematics in cryptology. This is particularly true for the theory of permutations, known since over a hundred years (1) , called formerly the theory of substitutions . Its application by Polish cryptologists enabled, in turn of years 1932-33, to break the German Enigma cipher, whichh subsequently exerted a considerable influence on the course of 1939-1945 war operation upon the European and African as well as the Far East war theatres (see [1]-[4]). The present paper is intended to show, necessarily in great brevity and simplification, some aspects of the Enigma cipher breaking, those in particular which used the theory of permutations. This paper, being not a sistematic outline of the process of breaking the Enigma cipher, presents however its important part.
It should be mentioned that the present paper is the first publication on the mathematical background on the Enigma cipher breaking. There exist, however, several reports related to this topic by the same author: one - written in 1942 - can be found in the General Wladyslaw Sikorski Historical Institute in London. and the other - written in 1967 - is deposited in the Military Historical Institute in Warsaw.

|
Phot. 1 |
1. Description of the machine . Enigma, a work of the German engineer Scherbius, is an electromechanical device. Phot. 1 gives an image of the machine and enables the description of its operation to be abbreviated.
Enigma has a 26-letter keyboard behind which a board with 26 letters illuminated from below with bulbs is located. The main ciphering device, partially visible in the photograph, consists of three ciphering drums put on a common axle and a fourth - a stationary one - the so called reverting drum witch with the use of a lever can be shifted toward and outward of the ciphering drums. The three ciphering drums carry upon their circumferences the letters of the alphabet (Phot.2), the upper of witch are visible by small windows of a lid. Alongside there are seen, protruding a bit, handles enabling manipulations with the drums. Each of the three ciphering drums has on its one side 26 concentric fixed contacts and of the other side - 26 spring contacts. The fixed contacts are connected with the spring contacts in an irregular way with the use of insulated wires housed within the ebonite boxes of drums. The reverting drums has spring contacts only and they are connected in pairs, also in an irregular way. The connections of the four drums form the main ciphering part and are the main secret of Emigma. The block diagram of the electric circuit with drums and other parts nad their notation is shown i Fig. 1. On the right of the drums a dry battery of low voltage (4 V) is placed, in front of the machine, before the keyboard, there is a device like a telephon switch-board. Six pairs of plugs with connecting cords enable an interchange of 12 among 26 letters of the alphabet.

|
| Phot. 2 |
Pressing a key cause the right drum to turn by the 1/26th of the round angle. Simultaneously, the electric circuit is closed for the current flowing from the pressed key through the plugboard, all three ciphering drums, the reverting drum and back through the ciphering drums and again through the plugboard. One of the bulbs is shining then and there can be seen a letter which is different from that on the pressed key. If, in the preceding position of the drum, the key marked with the letter illuminated just now had been pressed, then the bulb marked with the same letter as the previous key would shine.The enigma machine serves thus both for changing the plain text into the ciphered one and for the reverse transformation without need of any additional manipulations. Each subsequent pressing of a key causes the rotation of the right drum by the 1/26th of the round angle to be continued and another bulb to be shone. The middle and the left drums also rotate but much less frequently and their rotations will be negleeted in our considerations.
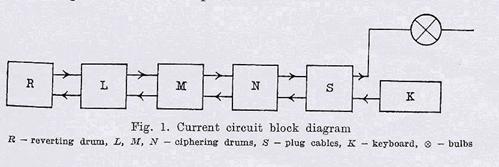
|
2. The way of ciphering . The Enigma ciphering machine can be used in many ways. In Germany military and paramilitary units till September 15, 1938, the following regulations were obeyed: the criptographer set first the drums to be prescribred, valid for a given day, basic position and performed reccomended changes of letters on the plugboard by putting the plugs into suitable sockets. Next, he chose the individual key for a message, consisting of three letters which were ciphered twice, thus obtaining six letters placed at the beginning of the message. Thus the individual keys for the given day had the following properties:
(1) all individual message keys were ciphered in the same basic position unknown to the cryptologist;
(2) each individual key was ciphered twice, so that the first letter meant the same as the fourth, the second - the same as the fifth and so on.
If a sufficent number of messages (approximately 80) of the same day are available, then, in general, all alphabet letters are present in their six initial places. In each place of the message they form a one-to-one transformation of the set of letters on itself and hence are permutations. These permutations, denoted subsequentely by letters from A to F , are unknown to the cryptologist. But the transitions from the first letter of each message to the fourth one, from the second to the fifth and from the third to the sixth form also permutations which, contrary to the previous ones, are entirely known to the cryptologist since they are the products AD, BE, CF of the above mentioned permutations. They can be represented as the products of disjoint cycles, and then take a very characteristic form, different, in general, for each day, e.g.
AD = (dvpfkxgzyo) (eijmunqlht) (bc) (rw) (a) (s)
(1) BE = (blfqveoum) (hjpswizrn) (axt) (cgy) (d) (k)
CF = (abviktjgfcqny) (duzrehlxwpsmo) .
Such a set of permutation resulting from the beginnings of messages forms a key for the Enigma secret.By the use of such sets for a few days only, it was possible to reconstruct the whole machine and afterwards each set enabled to reconstruct the keys changed daily in many years and thus to read messages ciphered with Enigma. We will pay more attention to this set due to its importance.
We know from the description of the machine that if the pressure of key, say x , causes a bulb y to shine, then, in turn, pressing the key y causes a bulb x to shine, whichh is obviously connected with the operation of the reverting drum. This is the reason why the all unknown permutations from A to F consist only of transpositions. If the criptographer in ciphering twice the individual key had pressed in the first place an unknon key x to receive the letter a and had pressed the same key x in the fourth place to receive the letter b , then by pressing in the first place the key a he should receive the letter x , and by pressing in the fourth place the key x - the letter b . Hence we have the successive operation: a onto x and then x onto b, which is called multiplications of permutations . So we see that by writing consecutively the letters ab we obtain a fragment of the permutation AD which is a product of unknown permutations A and D .
Let us take yet a small example. Let
dmq vbn, von puy, puc fmq
denote the beginnings, i.e. the twice-ciphered initial keys of three among approximately 80 messages obtained of a given day. From the first and fourth letters we see that d is substituted for v , v for p , and p for f . In this way we get a fragment of permutation AD , namely dvpf . In the same way from the second and fifth letters we see that o is substituted for u , u for m , and m for b . We get a fragment of permutation BE, namely oumb. And, finally, from the third and sixth letters we see that c is substituted for q , q for n , and n for y. We get a fragment of permutation CF, namely cqny. The beginnings of further messages enable to collect the complete permutations AD, BE, CF . This set, due to its form and primary importance, will be called the characteristic set or, directly, the characteristic of a given day .
3. The set of equations. As was explained, after the pressing of any key the current flows through a chain of machine devices before causing a particular bulb to shine. Each of these devices gives a permutation of letters. Let us denote by S the permutation caused by the plugboard, by L, M, N - those caused by the three ciphering drums, respectively, and by R - that caused by the reverting drum. The the passage of the current is described by the product of permutations SNMLRL -1 M -1 N -1 S -1 . But at the moment of pressing the key the drum N rotates by 1/26 th of its circumference. To consider this rotation, we introduce a special permutation (denoted always by P ) consisting of a single cycle which transforms each letter to the next letter:
P = (a b c d e f g h i j k l m n o p q r s t u v w x y z).
Fig.2, in which the ciphering part of the machine, i.e. the drums, is replaced by a 2-dimensional sliders, permits to follow the path of the current before and after shifting the drum N .
From the figure we read easily that the unknown permutations from A to F can be represented in the form
A = SPNP -1 MLRL -1 M -1 PN -1 P -1 S -1
B = SP 2 NP -2 MLRL -1 M -1 P 2 N -1 P -2 S -1
.....................................................
E = SP 5 NP -5 MLRL -1 M -1 P 5 N -1 P -5 S -1
F = SP 6 NP -6 MLRL -1 M -1 P 6 N -1 P -6 S -1
While the known products AD, BE, CF are given by the formulas
AD = SPNP -1 MLRL -1 M -1 PN -1 P 3 NP -4 MLRL -1 M -1 P 4 N -1 P -4 S -1
BE = SP 2 NP -2 MLRL -1 M -1 P 2 N -1 P 3 NP -5 MLRL -1 M -1 P 5 N -1 P -5 S -1
CF = SP 3 NP -3 MLRL -1 M -1 P 3 N -1 P 3 NP -6 MLRL- 1 M -1 P 6 N -1 P -6 S -1 .
The first part of our task is, in principle, to solve this set of equations in which the left-hand sides are known and the permutation P and its powers on the right -hand sides as well, whereas the permutations S, L, M, N, R are unknown. Since in this form the set is certainly unsolvable, we have to simplify it.
The first step in this direction is purely formal and consists of the substitution of a letter Q for the repeated product MLRL -1 M -1 , which can be interpreted as an equivalent reverting drum. Thus the number of unknowns is actually reduced to three: S, N, Q . Now we have
AD = SPNP -1 QPN -1 P 3 NP -4 QP 4 N -1 P -4 S -1
BE = SP 2 NP -2 QP 2 N -1 P 3 NP -5 QP 5 N -1 P -5 S -1
CF = SP 3 NP -3 QP 3 N -1 P 3 NP -6 QP 6 N -1 P -6 S -1 .
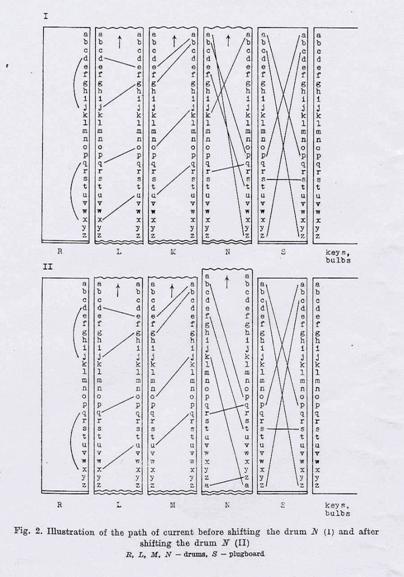
|
4. Theorem on the product of transpositions . The next step is more important. We aim to get disjoint unknown permutations from A to F from known products AD, BE, CF . As we explained earlier, the unknown permutations consists only of transpositions, and the expressions AD, BE, CF are their products. We can apply the following
THEOREM. If two permutations of the same degree consist only of disjoint transpositions, then their product contains an even number of disjoint cycles of the same lengths.
Proof. Let X and Y stand for the permutations to be multiplied and let their degree be 2n . If in the permutation X a transposition identical with a transposition in Y , e.g. (ab) , incidentally occurs, then in the product XY a pair of single-letter cycle (a)(b) will be observed. With respect to transpositions, identical in the two permutations, the theorem is thus true. After rejecting identical transpositions we can assume, without loss of generality, that the follow transpositions occur:
In permutation X in permutation Y
(a 1 a 2 ) (a 2 a 3 )
(a 3 a 4 ) (a 4 a 5 )
............. .............
(a 2k-3 a 2k-2 ) (a 2k-2 a 2k-1 )
(a 2k-1 a 2k ) (a 2k a 1 )
Indeed, the initial letter a 1 must finally appear in the permutation Y . When we perform the operation of multplying XY , we will always get two cycles of the same length k £ n :
(a 1 a 3 ... a 2k-3 a 2k-1 ) (a 2k a 2k-2 ... a 4 a 2 )
If in this way not all letters of the permutation are exhausted, we continue our procedure to exhaust all the letters.
Simultaneously we note that:
(1) the letters of a given transposition are always observed in two different cycle of the same length in the permutation XY ;
(2) if two letters appearing in two different cycles of the same length in the permutation XY belong to the same transposition, then their neighbouring letters (the left neighbour and the right one) belong to the same transposition.
The reverse theorem is particulary important:
If any permutation of even degree there appears an even number of disjoint cycles of the same length, then the permutation can be regarded as a product of two permutations each of which consist only of disjoint transpositions.
There is neither a need do develop a proof to the quoted reverse theorem nor a formula for the number of possible solutions for X and Y . It suffices to mention that this theorem – applied to the products AD , BE, CF – provides for each of the expressions A, B, C, depending on the form of the products, over ten or several tens possible solutions, while the permutations D, E, F are uniquely determined by them. For the whole characteristic set of three equations we get several thousands or several tens of thousands of possible solutions, thus choosing the actual one would be a difficult task.
The theorem on the product of transpositions does not lead us to the point we are aiming to get at, it brings us, however, to the proximity of it.
Let us assume, for example, that we know that the cryptographers prefer the same three letters, e.g. jjj , as the initial keys. If xqr gve are the initial key of a ciphered message, then making use of the characteristic set (1) and of the assumption that these letters mean jjj in the plain text we conclude, e.g. that the letters nfa qqb and eug imf , as the beginnings of messages, mean the letters ppp and zzz, respectively.
In this way, an accurate knowledge of preferences of the cryptographers together with the theorem of the product of transpositions enables us to find the only actual solution. Finally, the left-hand sides in the set of equations
A = SPNP -1 QPN -1 P -1 S -1
B = SP 2 NP -2 QP 2 N -1 P -2 S -1
(2) .......................................
E = SP 5 NP -5 QP 5 N -1 P -5 S -1
F = SP 6 NP -6 Q 1 P 6 N -1 P -6 S -1
can be regarded as known.
If the enquiring reader asks how the cryptologist knows – before breaking the cipher – the preferences of the cryptographers, we can reply that the cryptologist does not know these preferences but he tries to compensate his ignorance with long tests, imagination, and sometimes with an once of luck.
5. Connections of the drum N . It is not known to the author whether the set of six equations (2) with three unknown permutations S, N, Q is solvable without further data. It is known, however, that the set would become solvable if the cryptologist had at his disposal the messages from two different days with different connections on the plugboard, but with the same or similar setting of drums. At the first glance such a requirement seems to be quite fantastic, since the number of different settings of drums is, as will be explained later, 6 × 26 × 26 × 26 = 105456. Probability theory implies however that in several hundred days a pair of days with the same drum setting can be expected. Such a pair can be recognized as having the same characteristics (but not conversly: the same characteristics do not guarantee the same setting of drums for both days). However, if even such a pair of days were known, the way of solving the set of equations would still be long and a lot of cases should be checked. In any case, however, the method of solving, at least in theory, exists.
Actually, the necessary supplementary data were received in another, much shorter way. In December 1932 the French Bureau of Ciphers supplied to the Polish Bureau of Ciphers confidential material containing the tables of German keys to Enigma including the plugged connections S to the plugboard. It was possible to transfer the permutation S as known to the left-hand side of the set of equations
S -1 AS = PNP -1 QPN -1 P -1
S -1 BS = P 2 NP -2 QP 2 N -1 P -2
.......................................
S -1 ES = P 5 NP -5 QP 5 N -1 P -5
S -1 FS = P 6 NP -6 QP 6 N -1 P -6
In this way we obtained the set of six equations with only two unknown permutations N and Q . As we will show, this set is solvable, but needs yet certain transformations. Before doing the transformations we expalain a problem of theory of permutations.
If we have three permutations G, H, T and
G = T -1 H T,
Then we say that the permutation G is transformed from the permutations H by the permutation T.
As is proved in the theory of permutations, there is no need to multiply the permutation H by T -1 from the left and next by T from the right to get the permutation G . It is sufficient to perform on the element of the permutation H the changes prescribed in the permutation T . Therefore, the permutation G and H are similar. Thus it follows that if T is assumed to be an unknown, then the equation G = T -1 H T is solvable if an only if the permutation G and H are similar and we get as many solutions for T as there are ways of writing the permutation G under H without changing the value of permutation G . In the case, however, where G (or H ) consists of transposition only, the number of solutions is very large. For example, foe 13! Transpositions there are 2 13 × 13! =51011754393600 solutions. However, just this case we have at hand, since each permutation from A to F consists of 13 transpositions. So – in order to eliminate transpositions – we have to introduce some changes. First we transform both sides of the consecutive equations by means of P, P 2 ,..., P 6 , respectively, and denote (for brevity) the left-hand sides of the corresponding equations by U,V,...Z . Thus
U = P -1 S -1 ASP = NP -1 QPN -1
V = P -2 S -1 BSP 2 = NP -2 QP 2 N -1
.......................................
Z = P -6 S -1 BSP 6 = NP -6 QP 6 N -1 .
Next we calculate the proucts:
UV = NP -1 (QP -1 QP)PN -1
VW = NP -2 (QP -1 QP)P 2 N -1
WX = NP -3 (QP -1 QP)P 3 N -1
XY = NP -4 (QP -1 QP)P 4 N -1
YZ = NP -5 (QP -1 QP)P 5 N -1
Eliminating the common expression QP -1 QP we get a set of four equations wit only one unknown NPN -1 :
VW = NP -1 N -1 (UV)NPN -1
WX = NP -1 N -1 (UW)NPN -1
XY = NP -1 N -1 (WX)NPN -1
YZ = NP -1 N -1 (XY)NPN -1
Proceeding accordingly to the method given earlier, we get from the first equation several tens of possible expression for NPN -1 depending on the form of permutation UV (or of VW, WX, XY, YZ , since all of these permutations must have the same form, as otherwise an error in calculations had occurred or the drum M was accidentally shifted). But we obtain the same number of solutions for NPN -1 from the second equation and one of the solutions must be identical with that derived from the first equation. Now the last two equations are not necessary. We compare the obtained solution for NPN -1 with the permutation P . In this way we get 26 possible solutions for N -1 not differing considerably between themselves and, after choosing one of them, we easily obtain N itself, i.e., the inner connections of the right drum.
6. Concluding remarks. The description of the machine presented at the beginning was simplified in order to illustrate the process of reconstructing the connections of the drum N . Actually, the machine and its operations were much more complicated. For example, besides of the three ciphering drums and the reverting drum, Enigma had also an entry drum which complicated greatly breaking the cipher. Moreover, the rings of the drums carryng the letters of the alphabet could be shifted with respect to the rest parts of drums, so that the knowledge of the basic position brought no information on the actual position of the inner part of drums. Not only the drum N could rotate, but – at a smaller rate – also the drums L and M , which caused an additional complication. Finally, it was possible to change the sequence of ciphering drums and due to that the number of possible combinations increased six times. However, this last complication gave an effect not forseen by the designers. It caused that each of the three ciphering drums was placed from time to time at the right side of the set of drums. So the method described for the reconstruction of the drum N could sequentially be applied for each of the drums, and in this way the entire reconstruction of the inner structure of the Enigma ciphering machine was possible.
PART II - THE INITIAL KEYS
1.Cyclometer. The reconstruction of the machine was a necessary condition for breaking the Enigma cipher and a continous deciphering, but it was not sufficient. Methods should be devised to reconstruct quickly the daily initial keys. In other words, the problem to be solved was the reverse one that described in Part I. While then the task involved a reconstruction of the machine if the initial keys were known for a certain period (from the French confidential material), in the next step it was necessary to reconstruct the initial keys if the machine was reconstructed. Again the theory of permutation was helpful.
As follows from formulas (1), the permutation S transforms only letters within cycle which appear in the permutations AD, BE, CF and leaves unchanged the form of the cycles. The permutations AD, BE, CF have a charcteristic form (see the example following formulas (1)) and a set of three such permutations of the same form of cycles does not appear very frequently.
The three ciphering drums can be put of the axle in six different positions and the drums themselves can take 26 × 26 × 26 = 17576 different positions. If it there possible to find a device which for each position of drums gave the length and the number of cycles in the characteristics, and if the lengths and numbers of cycles were catalogued, then it would be sufficient to compare the products AD, BE, CF for a given day with the products of the same form in the catalogue to obtain immediately the proper sequence of drums and the permutation S , while the remaining elements of the daily initial key could be reconstructed by another method.
Such a device, called cyclometer , was really found and its unusual simplicity of design was striking. The cyclometer is illustrated in Fig. 3. Its main part consists of two assemblies (I and II) of ciphering drums connected with leads through whichh current flows, the drum N of the assembly II being shifted by three letters with respect the drum N of the assembly I, while the drums L and M of the assembly II are always in the same position as the drums L and M of the assembly I. Fig. 4 illustrates the principle of operation of the cyclometer.
For sake of simplicity the sequence of drums in the assembly II is reversed which, however, does not change the matter. The reverting drums are denoted by Q . They are equivalent (in the diagram only) to the drums R, L and M . Between the assemblies I ad II there is a system with bulbs and switches. If for any of the bulbs, e.g. l , the source of current (denoted by ¸ in the diagram) is switched on, then the current flows alternately through the assemblies I and II, and after a certain number of turns it comes back to the bulb l . All the bulbs in the circuit are then shining simultaneously. Their number, always even, is equal to the doubled number of letters in one of the cycles of permutation AD . After switching the source of current and closing in this way the circuit of another bulb not shining yet, further bulbs will shine, the number of which allows us to calculate the length of the next cycles in the permutation. In this manner, by rotating successively the drums and counting the number of lighting up bulbs, we can determine the length and the number of cycles in the characteristics for all 17576 drum positions for a given sequence. Since there are six possible sequences, the catalogue of characteristics include 6 × 17576 = 105456 positions altogether. The cyclometer was equipped with a variable resistor, since – due to incessantly changing number of shining points – bulbs had not lit up or they would blow.
2. Perforated charts. The cyclometer, or rather the catalogue of characteristics based on it, accomplished its task till September 15, 1938, and since that date in all of German units using Enigma, with the exception of SD (Sicherheitsdienst), quite new regulations realted to ciphering the initial keys of messages got mandatory. Since that time the Enigma operator had to choose himself the basic position which was different for ciphering the individual key of each message and this basic position was placed without ciphering (as a plain text) in the message heading. The individual key of a message was, as previously, ciphered twice. In this way the first letter of the individual key meant as before the same as the fourth, the second as he fifth, etc., but the basic position now known to the cryptologist was different for each message. Now, for a given day there are no characteristics products AD, BE, CF , the form of which could be found in the catalogue, but the relations between the first and the fourth, the second and the fifth, the third and the sixth letter of the key still existed and this had be of use. If, e.g., the individual key after ciphering had the form pst pwa , i.e. the first letter was the same as the fourth (or the second as the fifth, otr the third as the sixth), then in terms of permutations this meant that in the produ.cts AD, BE or CF (if they existed) there appeared one-letter cycle, called fixed point of permutation . Since the length of the cycles in the products AD, BE , CF is invariant with respect of the transoformations by the permutation S , the presence or absence of the fixed points in the products is invariant with respect to those transoformations.
Instead of a catalogue of cycle lengths in products a catalogue of fixed points of a all 17576 possible products (for each sequence of drums in the set) had to be elaborated to enable a comparison with the fixed points in the individual keys of messages of a given day. There was, however, a difficulty in performing such a comparison. The basic positions for each key have been known, as now the cryptographer had to write them as a plain text in the message heading, however, since the rings at the drum circunferences could be rearranged, actually only the relativity distances of fixed points displayed in the given daily keys were available.
The fixed point occurred in the catalogue in approximately 40% of all permutation products and perforated on a long tape would form a certain pattern. The fixed points of the keys of a given day perforated on another tape according to their basic positions would give also a certain pattern and the task consisted of the determination of the place at which all the fixed points of the second tape would coincide with those of the first tape. But this task presented, at least at that time, great technical difficulties. Moreover, the first tape should have double length to enable sliding the second tape over it. However, another method has been found by H.Zygalski.
For all 26 positions of the drum L , paper sheet (rather thick), denoted by a to z , were prepared and a square divided into 51x51 smaller squares was drawn on each sheet. Along the sides of the square (or a rectangle) the letters from a to z and from a to y were placed. It was a kind of coordinate system in which the abscissae and ordinates of points denoted possible positions of the drums M and N , respectively, while the small square denoted the permutation corresponding to these positions with o without the fixed points. The cases with fixed pionts were perforated. Such a sheet (in reduced scale) was like that in Fig. 5.
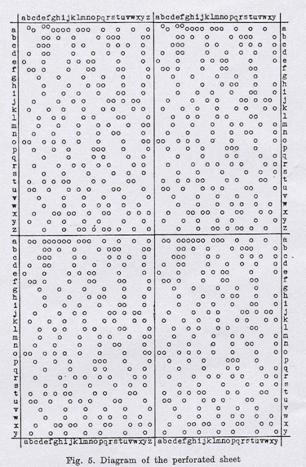
|
3. Concluding remarks. Besides the two methods of reconstructions of the keys, some other simple methods were in use, e.g. a so called grate method , together with mechanized and more expensive ones such as, e.g, the cryptologic bomb . They were used accordingly to the needs in different circumstances and time intervals, frequently treated as complementary to the cyclometer or to the perforated sheets. Different techniques and strategies were elaborated, with restricted range, but enabling to spare a lot of time and effort, such as a so-called clock method of J. Rozycki. As the German ciphering service introduced new and new obstacles to upset reconstruction of keys, it was necessary to counteract. So, on November 1, 1937, the reverting drum was changed to another, the number of cables in the plugboard increased gradually from 6 to 13 pairs, and on December 15, 1938, the number of the enciphering drums was increase from 3 to 5. The number of communication nets using the same enigma but with different keys was also gradually increased.
In September 1939 almost the whole equipment and the majority of files of the Ciphering Bureau were destroyed before and during the evacuation. However, after a meeting of the delegates of the Polish, the French and the British Ciphering Bureaus, held in Warsaw on July 25, 1939, the Polish side made available all its methods and the equipment for the Enigma deciphering to the allies together with copies of the German ciphering machine reconstructed in Poland with the use of theoretical investigations.
Notes
( 1) See, e.g., C. Jordan , Traitè des substitutions , Paris 1870.
References
[ 1] Gustave Bertrand , Enigma ou la plus grande énigme de la guerre 1939-1945 , Paris 1973.
[2] Wladyslaw Kozaczuk, Zlamany szyfr , Warszawa 1976.
[3] Wladyslaw Kozaczuk, Wojna w eterze, Warszawa 1977.
[4] F.W. Winterbotham, The Ultra Secret , London, 1974.
Typesetted version by Enrico Grigolon (November 2002).