Strong factorization property of Macdonald polynomials and higher-order Macdonald's positivity conjecture

Abstract

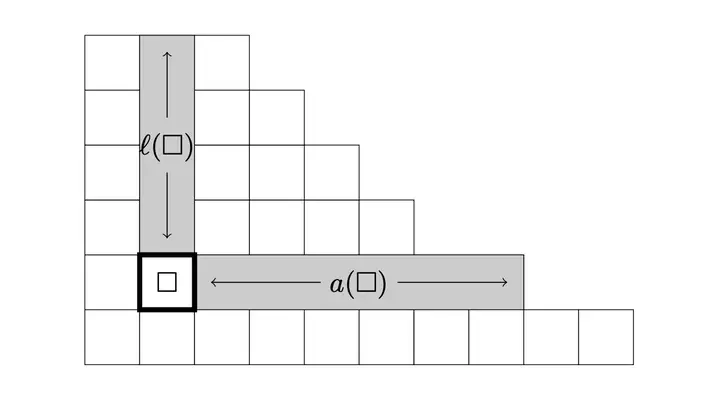
We prove a strong factorization property of interpolation Macdonald polynomials when $q$ tends to $1$. As a consequence, we show that Macdonald polynomials have a strong factorization property when $q$ tends to $1$, which was posed as an open question in our previous paper with Féray. Furthermore, we introduce multivariate $q,t$-Kostka numbers and we show that they are polynomials in $q,t$ with integer coefficients by using the strong factorization property of Macdonald polynomials. We conjecture that multivariate $q,t$-Kostka numbers are in fact polynomials in $q,t$ with nonnegative integer coefficients, which generalizes the celebrated Macdonald s positivity conjecture.