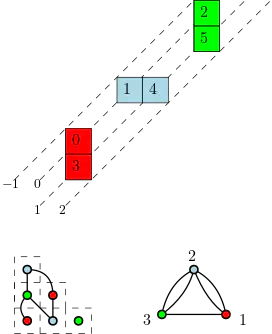
Abstract
The purpose of this note is to introduce a new family of quasi-symmetric functions called LLT cumulants and discuss its properties. We define LLT cumulants using the algebraic framework for conditional cumulants and we prove that the Macdonald cumulant has an explicit positive expansion in LLT cumulants of ribbon shapes, generalizing the classical decomposition of Macdonald polynomials. We also find a natural combinatorial interpretation of the LLT cumulant of a given directed graph as a weighted generating function of colorings of its subgraphs. We use this graph-theoretical framework to prove various positivity results. This includes monomial positivity, positivity in fundamental quasisymmetric functions and related positivity of the coefficients of Schur polynomials indexed by hook shapes. We also prove $e$-positivity for vertical-shape LLT cumulants, after the shift of variable $q \to q+1$, which refines a recent result of Alexandersson and Sulzgruber. All these results give evidence towards Schur-positivity of LLT cumulants, which we conjecture here. We prove that this conjecture implies Schur-positivity of Macdonald cumulants, and we give more evidence by proving the conjecture for LLT cumulants of melting lollipops, refining a recent result of Huh-Nam-Yoo.