Asymptotics of characters of symmetric groups: structure of Kerov character polynomials
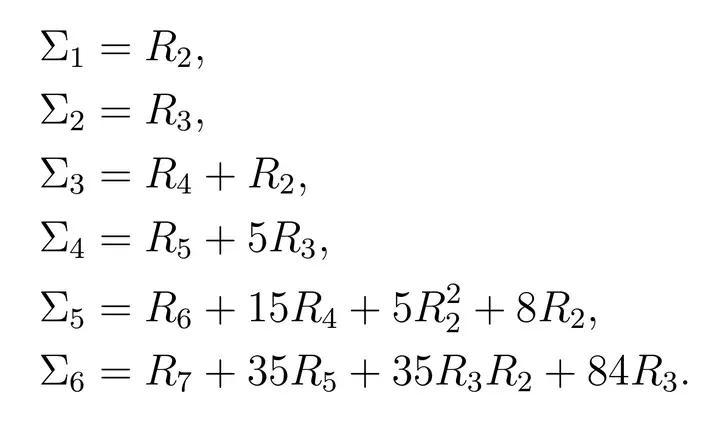
Abstract
We study asymptotics of characters of the symmetric groups on a fixed conjugacy class. It was proved by Kerov that such a character can be expressed as a polynomial in free cumulants of the Young diagram (certain functionals describing the shape of the Young diagram). We show that for each genus there exists a universal symmetric polynomial which gives the coefficients of the part of Kerov character polynomials with the prescribed homogeneous degree. The existence of such symmetric polynomials was conjectured by Lassalle.
Type
Publication
J. Combin. Theory Ser. A, 119 (6), 1174-1193, 2012