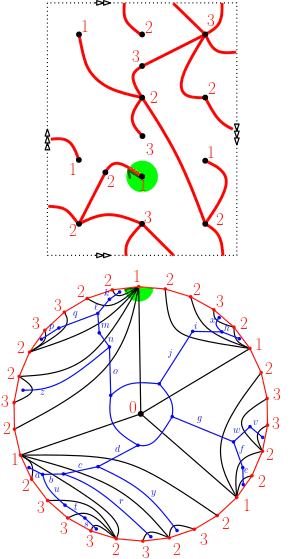
Abstract
We extend the Marcus-Schaeffer bijection between orientable rooted bipartite quadrangulations (equivalently: rooted maps) and orientable labeled one-face maps to the case of all surfaces, that is orientable and non-orientable as well. This general construction requires new ideas and is more delicate than the special orientable case, but it carries the same information. In particular, it leads to a uniform combinatorial interpretation of the counting exponent $\frac{5(h-1)}{2}$ for both orientable and non-orientable rooted connected maps of Euler characteristic $2-2h$, and of the algebraicity of their generating functions, similar to the one previously obtained in the orientable case via the Marcus-Schaeffer bijection. It also shows that the renormalization factor $n^{1/4}$ for distances between vertices is universal for maps on all surfaces: the renormalized profile and radius in a uniform random pointed bipartite quadrangulation on any fixed surface converge in distribution when the size $n$ tends to infinity. Finally, we extend the Miermont and Ambj"orn-Budd bijections to the general setting of all surfaces. Our construction opens the way to the study of Brownian surfaces for any compact 2-dimensional manifold.