Secant Varieties Working Group
(follow up to Secant Varieties Working Group of Varieties: Arithmetic and Transformations)
|
in the winter semester of 2021/2022 meetings take place on:
Wednesday 11:30-13:00, room 403
|
Research problems we try to address:
- Find membership test for secant variaties which do not apply for cactus varieties.
The initial work of the group in this direction is now available at arxiv: https://arxiv.org/abs/2007.16203
- For a fixed tensor
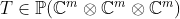 find criteria for find criteria for 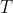 to have border rank equal to to have border rank equal to 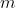 . (Arpan Pal from Texas A&M University is also working on this topic . (Arpan Pal from Texas A&M University is also working on this topic
https://www.math.tamu.edu/~arpantamu/)
- High rank loci. For
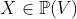 let let 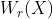 be the closure of tensors in be the closure of tensors in 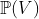 which have rank equal to which have rank equal to  . Is there an equality between . Is there an equality between 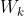 and and 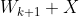 for for 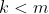 , where , where 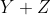 denotes the join of denotes the join of 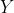 and and 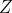 ? (answer is no - recently solved by E. Ballico, A. Bernardi, E. Ventura ? (answer is no - recently solved by E. Ballico, A. Bernardi, E. Ventura
- For
 , where , where 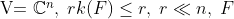 is generic from is generic from 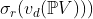 we want to find decomposition we want to find decomposition 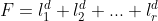 for for 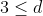 . We would like to find an algorithm wich computes such a decomposition. . We would like to find an algorithm wich computes such a decomposition.
- For
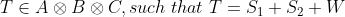 where where 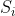 are simple tensors with norm are simple tensors with norm 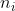 and and 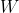 is a random error with norm is a random error with norm 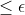 . Assuming . Assuming 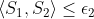 we want to find the funcition we want to find the funcition 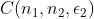 such that such that 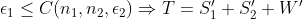 is the best rank 2 approximation and the norms is the best rank 2 approximation and the norms 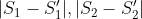 are bounded from above by some constant. are bounded from above by some constant.
- Find a generic rank for a partially symmetric tensors over Segre-Veronese varieties.
- Find the dimension of a secant variety to Segre-Veronese varieties.
- Border rank of monomials. We are looking for a generalisation of the Ranestad-Schrayer bound to multiprojective spaces.
- Other variants of Comon's and Strassen's conjectures. For example, symmetric Strassen conjecture, cactus version of Comon's conjecture, border version of Comon's conjecture.
We are open to discuss any issues related to secant varieties, cactus varieties, tensor rank, Waring rank, and their border/cactus analogues, identifiability, apolarity, Hilbert schemes of points etc.
|